Regex and quotient construction

Question 1

Give regular expressions for the languages below

$L = \{ a^n b^m \mid (n+m)\%2 = 0 \}$

$\boxed{(aa)^{*}(bb)^{*} + a(aa)^{*}b(bb)^{*}}$

$L = \{ w \mid w \text{ does not contain the substring: } aba \}$

$\boxed{b^{*}a^{*}((bb)b^{*}a^{*})^{*}b^{*}}$

$L = \{ w \mid w \text{ has an even number of } b's \}$

$\boxed{(a^{*}ba^{*}b)^{*} a^{*}}$

Question 2

Minimize the number of states in DFA via quotient construction.

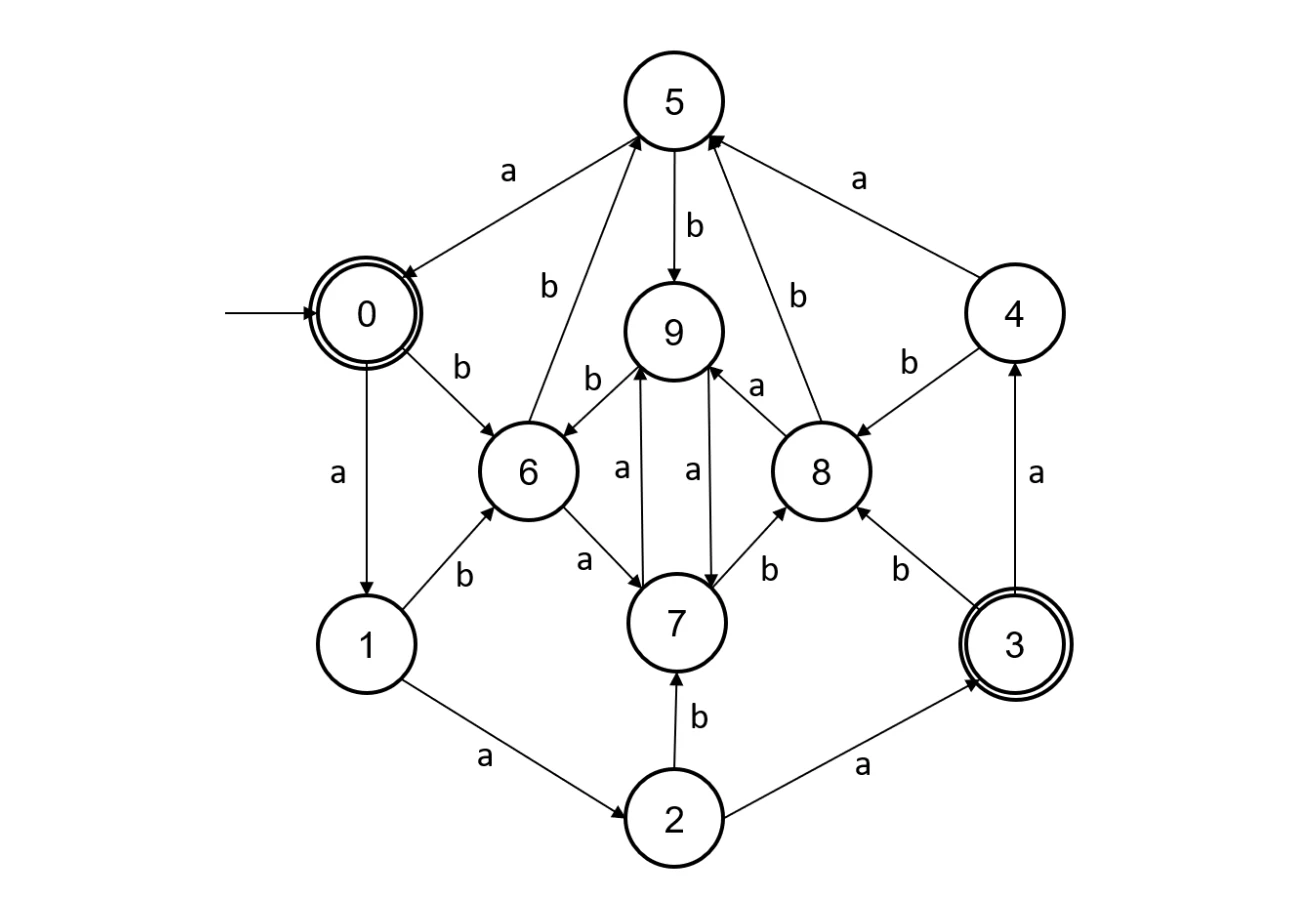
Note that all newly marked notes will be highlighted yellow.

Initial setup

Iteration 1:

• $(\delta (0,a), \delta (3,a)) = (1,4)$, which is unmarked, skipped

Iteration 2:

• $(\delta (1,a), \delta (2,a)) = (2,3)$, which is marked, mark $(1,2)$
• $(\delta (1,a), \delta (4,a)) = (2,5)$, which is unmarked, skipped
• $(\delta (1,a), \delta (5,a)) = (2,0)$, which is marked, mark $(1,5)$
• $(\delta (1,a), \delta (6,a)) = (2,7)$, which is unmarked, skipped
• $(\delta (1,a), \delta (7,a)) = (2,9)$, which is unmarked, skipped
• $(\delta (1,a), \delta (8,a)) = (2,9)$, which is unmarked, skipped
• $(\delta (1,a), \delta (9,a)) = (2,7)$, which is unmarked, skipped

Iteration 3:

• $(\delta (2,a), \delta (4,a)) = (3,5)$, which is marked, mark $(2,4)$
• $(\delta (2,a), \delta (5,a)) = (3,0)$, which is unmarked, skipped
• $(\delta (2,a), \delta (6,a)) = (3,7)$, which is marked, mark $(2,6)$
• $(\delta (2,a), \delta (7,a)) = (3,9)$, which is marked, mark $(2,7)$
• $(\delta (2,a), \delta (8,a)) = (3,9)$, which is marked, mark $(2,8)$
• $(\delta (2,a), \delta (9,a)) = (3,7)$, which is marked, mark $(2,9)$

Iteration 4:

• $(\delta (4,a), \delta (5,a)) = (5,0)$, which is marked, mark $(4,5)$
• $(\delta (4,a), \delta (6,a)) = (5,7)$, which is unmarked, skipped
• $(\delta (4,a), \delta (7,a)) = (5,9)$, which is unmarked, skipped
• $(\delta (4,a), \delta (8,a)) = (5,9)$, which is unmarked, skipped
• $(\delta (4,a), \delta (9,a)) = (5,7)$, which is unmarked, skipped

Iteration 5:

• $(\delta (5,a), \delta (6,a)) = (0,7)$, which is marked, mark $(5,6)$
• $(\delta (5,a), \delta (7,a)) = (0,9)$, which is marked, mark $(5,7)$
• $(\delta (5,a), \delta (8,a)) = (0,9)$, which is marked, mark $(5,8)$
• $(\delta (5,a), \delta (9,a)) = (0,7)$, which is marked, mark $(5,9)$

Iteration 6:

• $(\delta (6,a), \delta (7,a)) = (7,9)$, which is unmarked, skip
• $(\delta (6,a), \delta (8,a)) = (7,9)$, which is unmarked, skip
• $(\delta (6,a), \delta (9,a)) = (7,7)$, which is unmarked, skip

We stopped here, given that 7,8,9 doesn’t contains any direct transition on a to any final states.

The final transition table are as follows:

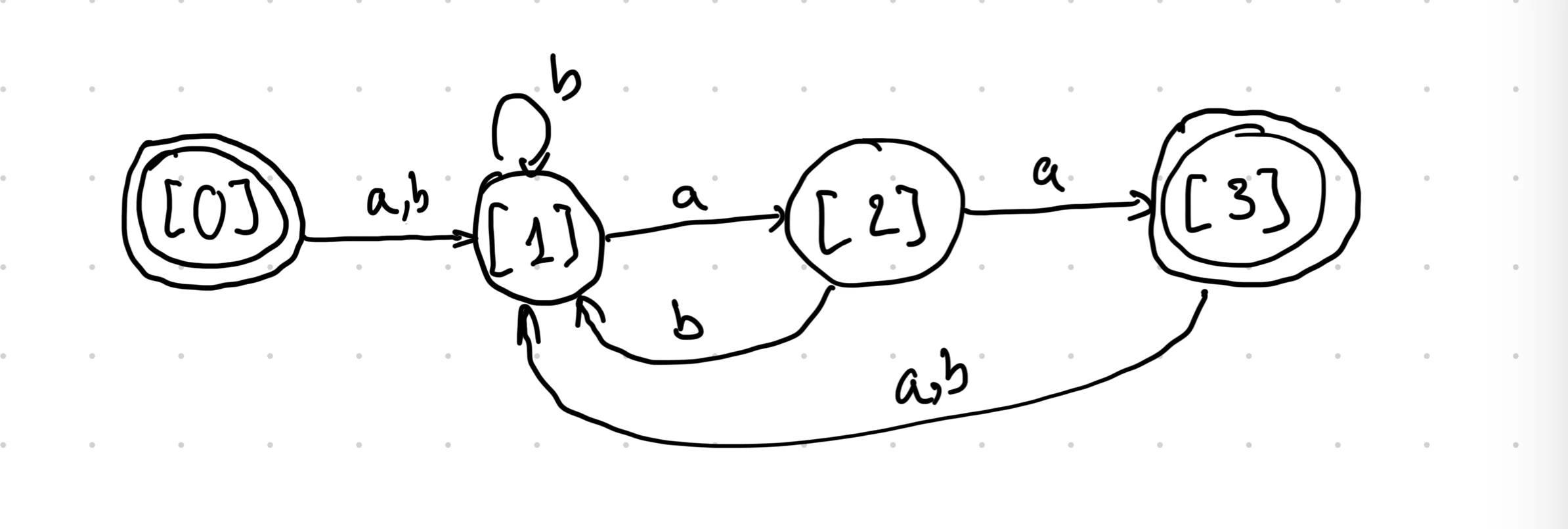
We have the following states are equivalent:

• $1 \approx 4 \approx 6 \approx 7 \approx 8 \approx 9$
• $2 \approx 5$

Final DFA

Question 3

Your friend is looking at the formal definition of the pumping lemma and they think something is wrong

$$L \text{ is regular } \implies (\exists k \mid k>0: (\forall x,y,z \mid xyz \in L \land |y| > k: ( \exists u,v,w \mid y=uvw \land v \neq \epsilon: (\forall i | i \geq 0: xuv^iwz \in L))))$$

They understand the argument it is crafted around, that is, due to the fact that strings are arbitrarily long and a DFA has finite states there must be a segment of accepted strings which “loop” in the machine. However, they claim for the pumping lemma above to hold, $L$ must be infinite, because if $L$ was finite the argument about “looping” no longer holds. Therefore, the pumping lemma only holds when $L$ is infinite.

You can see where your friend is coming from, but they are incorrect. Why? Be precise in your argument, that is, show how if $L$ is finite, then

$$(\exists k \mid k > 0: (\forall x,y,z \mid xyz \in L \land |y| > k: ( \exists u,v,w \mid y=uvw \land v \neq \epsilon: (\forall i | i \geq 0: xuv^iwz \in L))))$$

evaluate to true.

The Pumping lemma also holds for finite regular language as well.

We need to show that if we assume $L$ is finite, then the pumping lemma is True.

Now, there exists a longest string in L called $m$, choose $k^{'} = |m|$

Consider the “forall” section $\forall x,y,z \mid xyz \in L \land |y| >k$ is False:

• For any string $xyz \in L$ we know that $|xyz| \le m$ (since m is the longest string in $L$)
• since $y$ is a substring of $xyz$, we must have $|y| \le |xyz| \le m = k$

Given that the antecedent (“if” part) of an implication is false, the entire implication is vacuous truth (when the set is empty)

Therefore, the entire condition is true via vacuous truth (it holds trivially, as there are no strings $xyz \in L \mid |y| > k$)

Question 4

Using the Pumping Lemma, prove the following languages are not regular.

$L = \{ a^{nm} b^{m} a^{n} \mid n,m \ge 0 \}$

1. The demon first pick $k=n=m$
2. Choose $x=a^{k^{2}}, y=b^{k}, z=a^{k}$
3. pick $u=b^{j},v=b^{r},w=b^{l}$ such that $j+r+l=k, r>0$
4. pick $s^{'} = xuv^{i}wz = a^{k^{2}}b^{j}(b^{r})^{i}b^{l}a^{k}$ use $i=2$ we have $$\begin{aligned} s^{'}&=a^{k^{2}}b^{j}b^{2r}b^{l}a^{k} \\ &=a^{k^{2}}b^{r}b^{k}a^{k} \end{aligned}$$
5. That $s^{'} \notin L$, therefore $L$ is not regular

$\boxed{q.e.d}$

$L = \{ww \mid w \in \Sigma^*\}$

1. The demon pick k
2. Choose $x=a^{k}b,y=a^{k},z=b$
3. pick $u=a^{j},v=a^{r},w=a^{l}$ such that $j+r+l=k, r>0$
4. pick $s^{'} = xuv^{i}wz = a^{k}ba^{j}(a^{r})^{i}a^{l}b$ use $i=2$ we have $$\begin{aligned} s^{'}&=a^{k}ba^{j}a^{2r}a^{l}b \\ &=a^{k}ba^{r}a^{k}b \end{aligned}$$
5. That $s^{'} \notin L$, therefore $L$ is not regular

$\boxed{q.e.d}$

$L = \{a^{k^{3} } \mid k \ge 0\}$

1. The demon pick k
2. Choose $x=z=\epsilon,y=a^{k^{3}}$
3. pick $u=a^{j},v=a^{r},w=a^{l}$ such that $j+r+l=k^{3}, r>0, j+r\le k$
4. pick $s^{'} = xuv^{i}wz = a^{j}(a^{r})^{i}a^{l}$ use $i=2$ we have $$\begin{aligned} s^{'}&=a^{j}(a^{r})^{2}a^{l} \\ &=a^{k^{3}+r} \end{aligned}$$ We can prove that $k^{3} < k^{3}+r <(k+1)^{3}$
   • Since $r>0$, we have $k^{3}<k^{3}+r$
   • Given $r\le k$ therefore $(k+1)^{3} = k^{3}+3k^{2}+3k+1 > k^{3} + k \ge k^{3}+r$ Therefore, $k^{3}+r$ cannot be a perfect cube
5. That $s^{'} \notin L$, therefore $L$ is not regular

$\boxed{q.e.d}$

Question 5

Give the CFGs for the following language

$L = \{a^{n}b^{m}c^{k} \mid n \neq m + k\}$

$L = L_{1} \cup L_{2}$ where

• $L_{1} = \{a^{n}b^{m}c^{k} \mid n < m+k\}$
• $L_{2} = \{a^{n}b^{m}c^{k} \mid n > m+k\}$

Let grammar $G = (V, \Sigma, R, S)$ where:

• $V = \{S, S_{1}, S_{2}, A, B\}$ be set of variables
• $\Sigma = \{a,b,c\}$ be the set of terminals

$L=\{a^{n}b^{m}c^{k} \mid n = m+k\}$