PID Controller from input signals
Transfer function for angular speed:
A 1 + τ s \frac{A}{1 + \tau s} 1 + τ s A The input signal that begins at time t 0 t_{0} t 0 u min , u max u_\text{min}, u_\text{max} u min , u max
The resulting output signal is initially at y 0 y_{0} y 0 y ss y_\text{ss} y ss
The steady state gain A A A
A = y ss − y 0 u max − u min = △ y △ u A = \frac{y_\text{ss} - y_0}{u_\text{max} - u_\text{min}} = \frac{\triangle y}{\triangle u} A = u max − u min y ss − y 0 = △ u △ y Time constant τ \tau τ 0.632 × △ y 0.632 \times \triangle y 0.632 × △ y
Let t 1 t_1 t 1 0.632 × △ y 0.632 \times \triangle y 0.632 × △ y
y ( t 1 ) = 0.632 × ( y ss − y 0 ) + y 0 τ = t 1 − t 0 \begin{aligned}
y(t_{1}) &= 0.632 \times (y_\text{ss} -y_{0}) + y_{0} \\[8pt]
\tau &= t_{1} - t_{0}
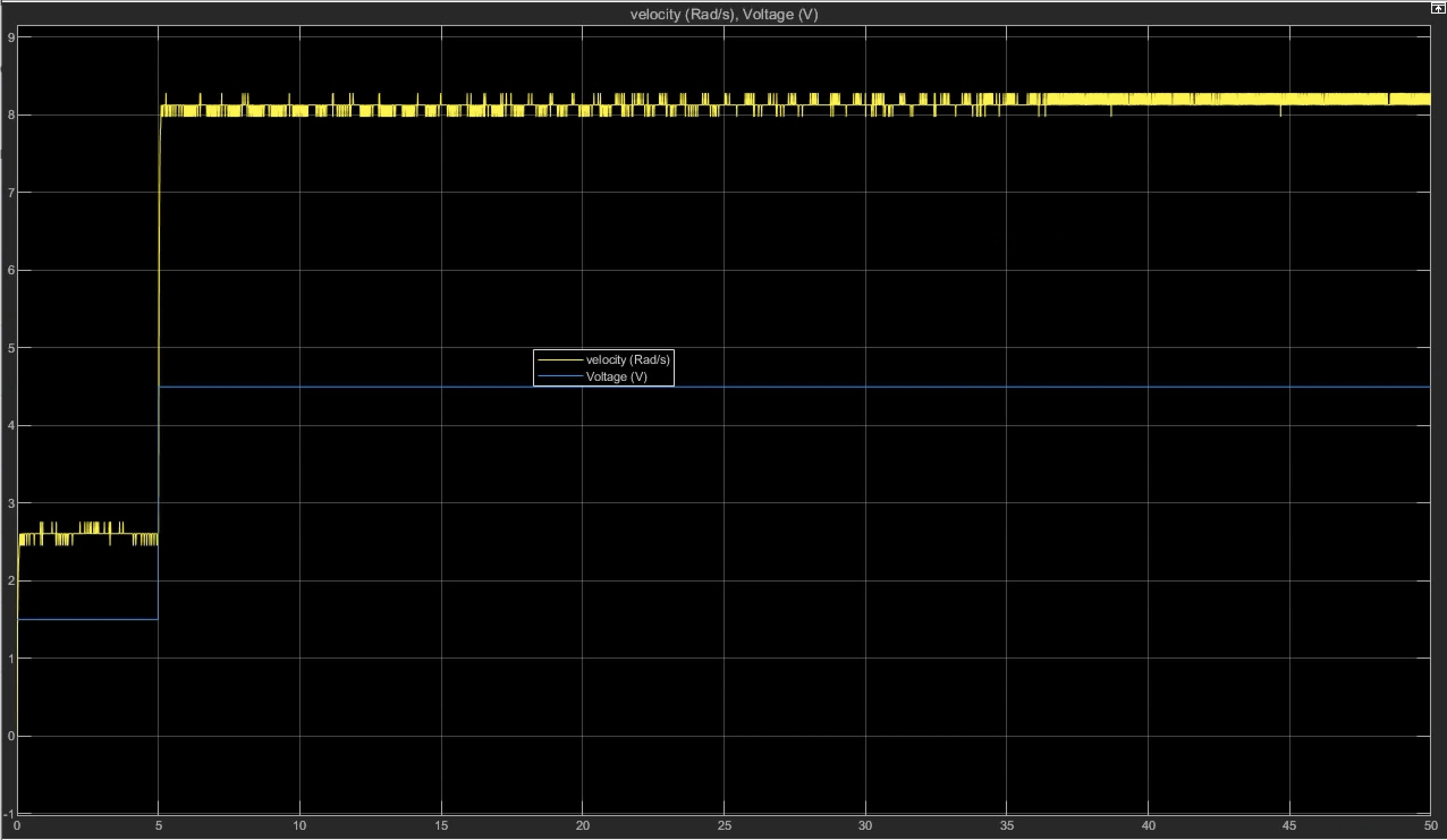
\end{aligned} y ( t 1 ) τ = 0.632 × ( y ss − y 0 ) + y 0 = t 1 − t 0 find the transfer function △ y = 3 V △ v = 8.285 − 2.454 = 5.831 rad/s A = 5.831 3 = 1.9436666667 rad/s target velocity = 2.454 + 0.632 ∗ 5.831 = 6.139192 rad/s τ ≈ 0.029 secs \begin{align*}
\triangle y &= 3V \\[6pt]
\triangle v &= 8.285 - 2.454 = 5.831 \text{rad/s} \\[6pt]
A &= \frac{5.831}{3} = 1.9436666667 \text{rad/s} \\[12pt]
\text{target velocity} &= 2.454 + 0.632 * 5.831 = 6.139192 \text{rad/s} \\[8pt]
\tau \approx 0.029 \text{secs}
\end{align*} △ y △ v A target velocity τ ≈ 0.029 secs = 3 V = 8.285 − 2.454 = 5.831 rad/s = 3 5.831 = 1.9436666667 rad/s = 2.454 + 0.632 ∗ 5.831 = 6.139192 rad/s note: reach it at around 5.029 sec
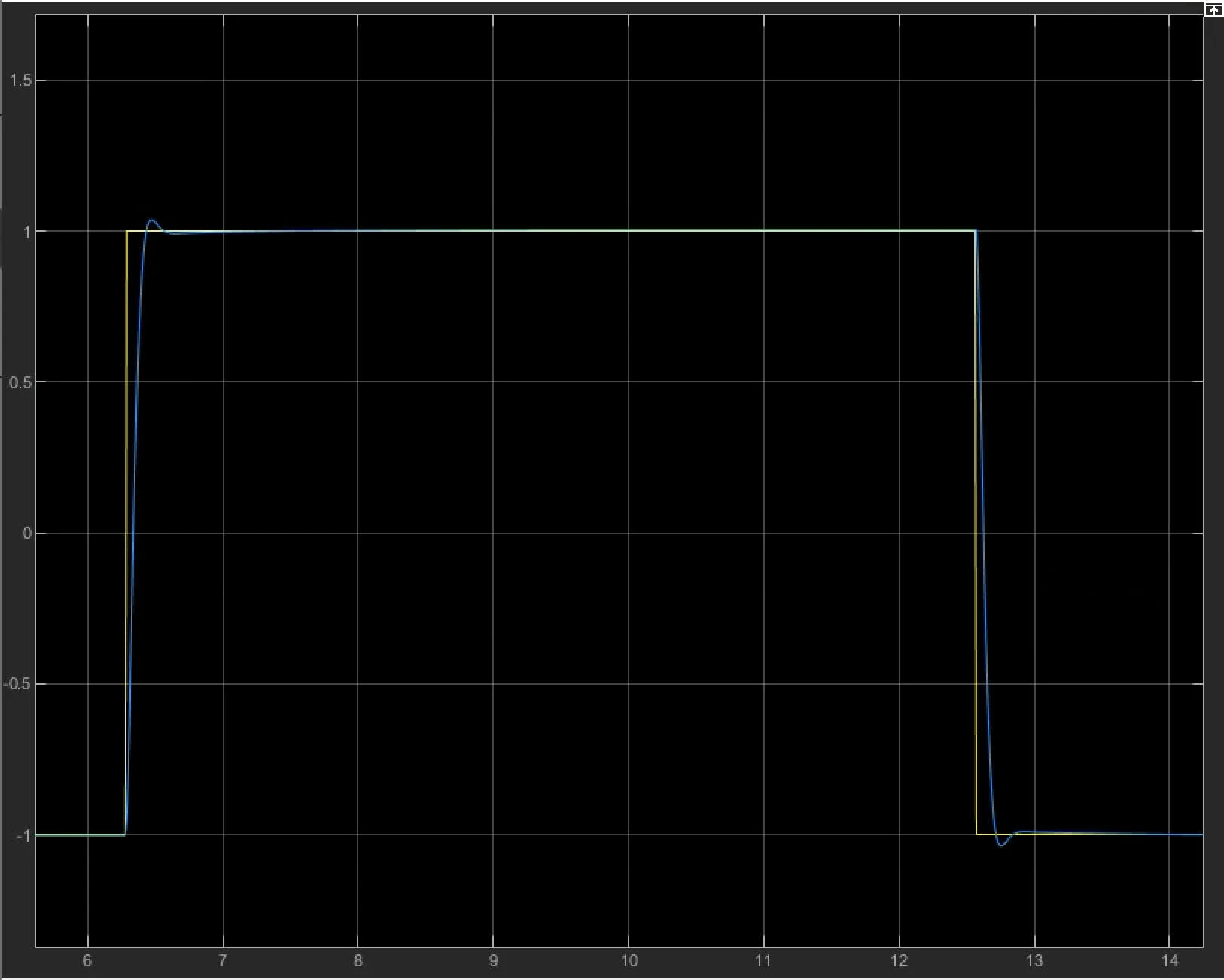
graphs see
proportional P = 350 ∗ π 180 P = 350 * \frac{\pi}{180} P = 350 ∗ 180 π
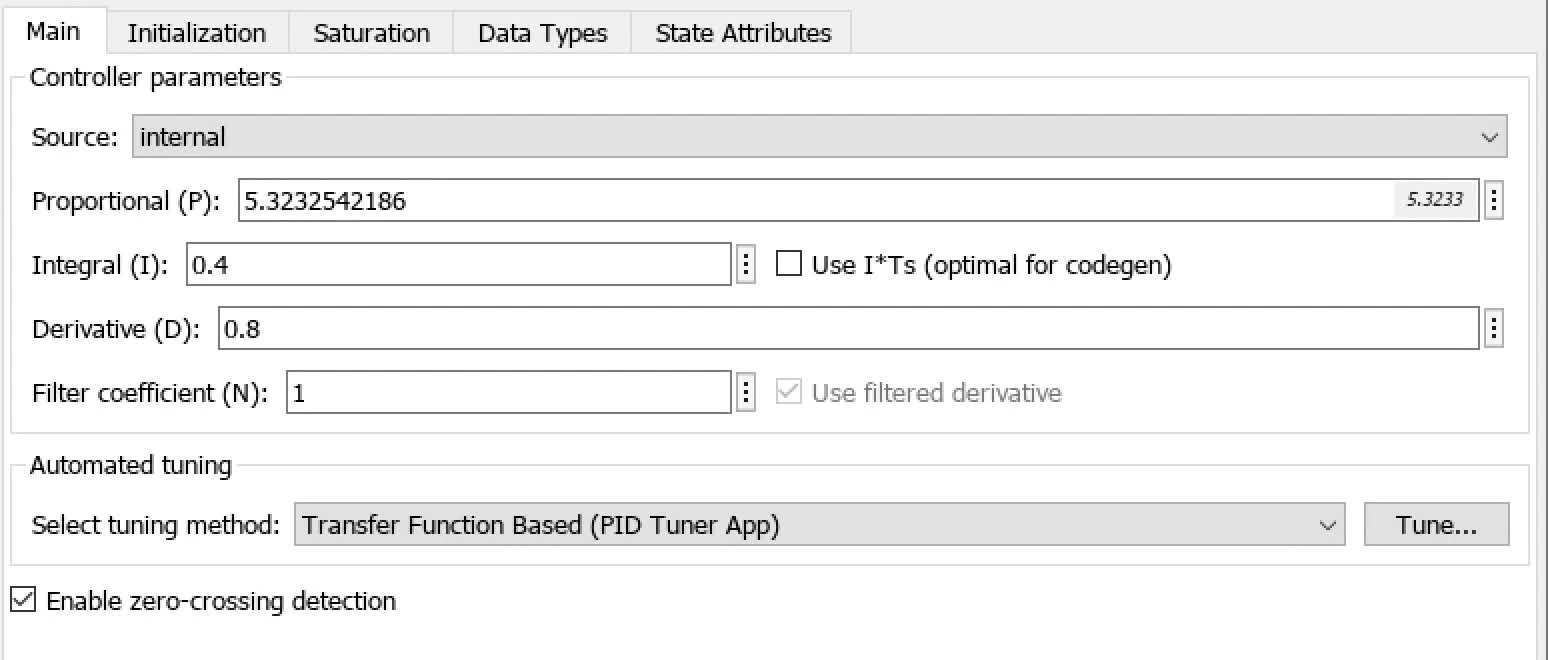 proportional
proportional