Graphs See also
Node as edges as relationship between
Directed acyclic graph (DAG) Application:
undirected.
( N , E ) (\mathcal{N}, \mathcal{E}) ( N , E )
N \mathcal{N} N E \mathcal{E} E undirected edges: E ⊆ N × N \mathcal{E} \subseteq \mathcal{N} \times \mathcal{N} E ⊆ N × N
path is a sequence of nodes and edges connect two nodes.
A graph is connected if there is a path between every pair of vertices.
In a weight undirected graph each edge has a weight: w : E → R w: \mathcal{E} \to \mathbb{R} w : E → R
See also
directed.
( N , E ) (\mathcal{N}, \mathcal{E}) ( N , E )
N \mathcal{N} N E \mathcal{E} E E ⊆ N × N \mathcal{E} \subseteq \mathcal{N} \times \mathcal{N} E ⊆ N × N
sequence of nodes and edges are directional, edges are ordered pairs.
path with at-least one edge from a node
Strongly component : maximal sub-graph in which all node pairs are strongly connected.
Let G = ( N , E ) \mathcal{G} = (\mathcal{N}, \mathcal{E}) G = ( N , E ) n ∈ N ∧ i d ( n ) with 0 ≤ i d ( n ) ≤ ∣ N ∣ n \in \mathcal{N} \land id(n) \text{ with } 0 \leq id(n) \leq |\mathcal{N}| n ∈ N ∧ i d ( n ) with 0 ≤ i d ( n ) ≤ ∣ N ∣
Let M = ∣ N ∣ × ∣ N ∣ M = | \mathcal{N} | \times | \mathcal{N} | M = ∣ N ∣ × ∣ N ∣
For every pairs of nodes ( m , n ) (m, n) ( m , n ) M [ i d ( m ) , i d ( n ) ] ≔ ( m , n ) ∈ E M[id(m), id(n)] \coloneqq (m, n) \in \mathcal{E} M [ i d ( m ) , i d ( n )] : = ( m , n ) ∈ E
The adjacency list representation
Let A [ 0 … ∣ N ∣ A \lbrack 0 \dots |\mathcal{N}| A [ 0 … ∣ N ∣ bags
For every edge ( m , n ∈ E ) (m, n \in \mathcal{E}) ( m , n ∈ E ) n n n ( m , n ) (m,n) ( m , n ) A [ i d ( m ) ] A \lbrack id(m) \rbrack A [ i d ( m )]
ops complexity add/remove nodes Θ ( ∥ N ∥ ) \Theta(\|\mathcal{N}\|) Θ ( ∥ N ∥ ) add/remove edges ( n , m ) (n, m) ( n , m ) Θ ( ∥ o u t ( n ) ∥ ) \Theta(\|out(n)\|) Θ ( ∥ o u t ( n ) ∥ ) check an edge ( n , m ) (n, m) ( n , m ) Θ ( ∥ o u t ( n ) ∥ ) \Theta(\|out(n)\|) Θ ( ∥ o u t ( n ) ∥ ) iterate over all incoming edges of n n n Θ ( ∥ E ∥ ) \Theta(\|\mathcal{E}\|) Θ ( ∥ E ∥ ) iterate over all outgoing edges of n n n Θ ( ∥ o u t ( n ) ∥ ) \Theta(\|out(n)\|) Θ ( ∥ o u t ( n ) ∥ ) Check or change the weight of ( n , m ) (n, m) ( n , m ) Θ ( 1 ) \Theta(1) Θ ( 1 )
comparison.
Dense graph: ∣ E ∣ ≈ Θ ( ∣ N ∣ 2 ) |\mathcal{E}| \approx \Theta(|\mathcal{N}|^2) ∣ E ∣ ≈ Θ ( ∣ N ∣ 2 ) Sparse graph: ∣ E ∣ ≈ Θ ( ∣ N ∣ ) |\mathcal{E}| \approx \Theta(|\mathcal{N}|) ∣ E ∣ ≈ Θ ( ∣ N ∣ )
Traversing undirected graph. Depth-first search (DFS) "\\begin{algorithm}\n\\caption{DFS-R(G, marked, n)}\n\\begin{algorithmic}\n\\REQUIRE $G = (\\mathcal{N}, \\mathcal{E}), \\text{marked}, n \\in \\mathcal{N}$\n\\FORALL{$ (n, m) \\in \\mathcal{E} $}\n \\IF{$\\neq \\text{marked}[m]$}\n \\STATE $\\text{marked}[m] \\coloneqq \\text{true}$\n \\STATE $\\text{DFS-R}{(G, \\text{marked}, m)}$\n \\ENDIF\n\\ENDFOR\n\\end{algorithmic}\n\\end{algorithm}"
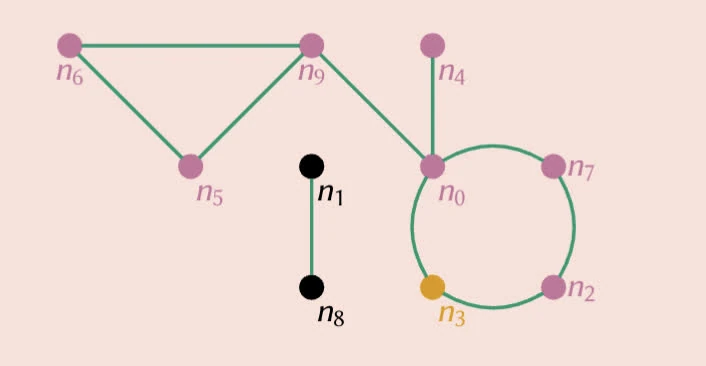
Algorithm 1 DFS-R(G, marked, n)
Require: G = ( N , E ) , marked , n ∈ N G = (\mathcal{N}, \mathcal{E}), \text{marked}, n \in \mathcal{N} G = ( N , E ) , marked , n ∈ N
1: for all ( n , m ) ∈ E (n, m) \in \mathcal{E} ( n , m ) ∈ E do
2: if ≠ marked [ m ] \neq \text{marked}[m] = marked [ m ] then
3: marked [ m ] ≔ true \text{marked}[m] \coloneqq \text{true} marked [ m ] : = true
4: DFS-R ( G , marked , m ) \text{DFS-R}{(G, \text{marked}, m)} DFS-R ( G , marked , m )
5: end if
6: end for
marked ≔ { n ⟼ ( n ≠ s ) ∣ n ∈ N } \text{marked} \coloneqq \lbrace n \longmapsto (n \neq s) \mid n \in \mathcal{N} \rbrace marked : = { n ⟼ ( n = s ) ∣ n ∈ N }
all nodes to which n 3 n_3 n 3
G \mathcal{G} G not a connected graphThe order of recursive call determines all n 3 n_3 n 3
Complexity
∣ N ∣ |\mathcal{N}| ∣ N ∣ marked and at-most ∣ N ∣ |\mathcal{N}| ∣ N ∣ inspect each node at-most once and traverse each edge once: Θ ( ∣ N ∣ + ∣ E ∣ ) \Theta(|\mathcal{N}| + |\mathcal{E}|) Θ ( ∣ N ∣ + ∣ E ∣ )
Connected-components "\\begin{algorithm}\n\\caption{DFS-CC-R(G, cc, n)}\n\\begin{algorithmic}\n\\REQUIRE $G = (\\mathcal{N}, \\mathcal{E}), cc, n \\in \\mathcal{N}$\n\\FORALL{$(n, m) \\in \\mathcal{E}$}\n \\IF{$cc[m] = \\text{unmarked}$}\n \\STATE $cc[m] \\coloneqq cc[n]$\n \\STATE $\\text{DFS-CC-R}(G, cc, m)$\n \\ENDIF\n\\ENDFOR\n\\end{algorithmic}\n\\end{algorithm}"
Algorithm 2 DFS-CC-R(G, cc, n)
Require: G = ( N , E ) , c c , n ∈ N G = (\mathcal{N}, \mathcal{E}), cc, n \in \mathcal{N} G = ( N , E ) , cc , n ∈ N
1: for all ( n , m ) ∈ E (n, m) \in \mathcal{E} ( n , m ) ∈ E do
2: if c c [ m ] = unmarked cc[m] = \text{unmarked} cc [ m ] = unmarked then
3: c c [ m ] ≔ c c [ n ] cc[m] \coloneqq cc[n] cc [ m ] : = cc [ n ]
4: DFS-CC-R ( G , c c , m ) \text{DFS-CC-R}(G, cc, m) DFS-CC-R ( G , cc , m )
5: end if
6: end for
"\\begin{algorithm}\n\\caption{COMPONENTS(G, s)}\n\\begin{algorithmic}\n\\REQUIRE $G = (\\mathcal{N}, \\mathcal{E}), s \\in \\mathcal{N}$\n\\STATE $cc \\coloneqq \\{ n \\mapsto \\text{unmarked} \\}$\n\\FORALL{$n \\in \\mathcal{N}$}\n \\IF{$cc[n] = \\text{unmarked}$}\n \\STATE $cc[n] \\coloneqq n$\n \\STATE $\\text{DFS-CC-R}(G, cc, n)$\n \\ENDIF\n\\ENDFOR\n\\end{algorithmic}\n\\end{algorithm}"
Algorithm 3 COMPONENTS(G, s)
Require: G = ( N , E ) , s ∈ N G = (\mathcal{N}, \mathcal{E}), s \in \mathcal{N} G = ( N , E ) , s ∈ N
1: c c ≔ { n ↦ unmarked } cc \coloneqq \{ n \mapsto \text{unmarked} \} cc : = { n ↦ unmarked }
2: for all n ∈ N n \in \mathcal{N} n ∈ N do
3: if c c [ n ] = unmarked cc[n] = \text{unmarked} cc [ n ] = unmarked then
4: c c [ n ] ≔ n cc[n] \coloneqq n cc [ n ] : = n
5: DFS-CC-R ( G , c c , n ) \text{DFS-CC-R}(G, cc, n) DFS-CC-R ( G , cc , n )
6: end if
7: end for
Two-colourability
A graph is bipartite if we can partition the nodes in two sets such that no two nodes in the same set share an edge.
"\\begin{algorithm}\n\\caption{DFS-TC-R(G, colors, n)}\n\\begin{algorithmic}\n\\REQUIRE $G = (\\mathcal{N}, \\mathcal{E}), \\text{colors}, n \\in \\mathcal{N}$\n\\FORALL{$(n, m) \\in \\mathcal{E}$}\n \\IF{$\\text{colors}[m] = 0$}\n \\STATE $\\text{colors}[m] \\coloneqq -\\text{colors}[n]$\n \\STATE $\\text{DFS-TC-R}(G, \\text{colors}, m)$\n \\ELSIF{$\\text{colors}[m] = \\text{colors}[n]$}\n \\STATE \\textbf{print} \"This graph is not bipartite.\"\n \\ENDIF\n\\ENDFOR\n\\end{algorithmic}\n\\end{algorithm}"
Algorithm 4 DFS-TC-R(G, colors, n)
Require: G = ( N , E ) , colors , n ∈ N G = (\mathcal{N}, \mathcal{E}), \text{colors}, n \in \mathcal{N} G = ( N , E ) , colors , n ∈ N
1: for all ( n , m ) ∈ E (n, m) \in \mathcal{E} ( n , m ) ∈ E do
2: if colors [ m ] = 0 \text{colors}[m] = 0 colors [ m ] = 0 then
3: colors [ m ] ≔ − colors [ n ] \text{colors}[m] \coloneqq -\text{colors}[n] colors [ m ] : = − colors [ n ]
4: DFS-TC-R ( G , colors , m ) \text{DFS-TC-R}(G, \text{colors}, m) DFS-TC-R ( G , colors , m )
5: else if colors [ m ] = colors [ n ] \text{colors}[m] = \text{colors}[n] colors [ m ] = colors [ n ] then
6: print "This graph is not bipartite."
7: end if
8: end for
"\\begin{algorithm}\n\\caption{TwoColors(G)}\n\\begin{algorithmic}\n\\REQUIRE $G = (\\mathcal{N}, \\mathcal{E})$\n\\STATE $\\text{colors} \\coloneqq \\{ n \\mapsto 0 \\mid n \\in \\mathcal{N} \\}$\n\\FORALL{$n \\in \\mathcal{N}$}\n \\IF{$\\text{colors}[n] = 0$}\n \\STATE $\\text{colors}[n] \\coloneqq 1$\n \\STATE $\\text{DFS-TC-R}(G, \\text{colors}, n)$\n \\ENDIF\n\\ENDFOR\n\\end{algorithmic}\n\\end{algorithm}"
Algorithm 5 TwoColors(G)
Require: G = ( N , E ) G = (\mathcal{N}, \mathcal{E}) G = ( N , E )
1: colors ≔ { n ↦ 0 ∣ n ∈ N } \text{colors} \coloneqq \{ n \mapsto 0 \mid n \in \mathcal{N} \} colors : = { n ↦ 0 ∣ n ∈ N }
2: for all n ∈ N n \in \mathcal{N} n ∈ N do
3: if colors [ n ] = 0 \text{colors}[n] = 0 colors [ n ] = 0 then
4: colors [ n ] ≔ 1 \text{colors}[n] \coloneqq 1 colors [ n ] : = 1
5: DFS-TC-R ( G , colors , n ) \text{DFS-TC-R}(G, \text{colors}, n) DFS-TC-R ( G , colors , n )
6: end if
7: end for
Breadth-first search (BFS) "\\begin{algorithm}\n\\caption{BFS(G, s)}\n\\begin{algorithmic}\n\\REQUIRE $G = (\\mathcal{N}, \\mathcal{E}), s \\in \\mathcal{N}$\n\\STATE $\\text{marked} \\coloneqq \\{ n \\mapsto (n \\neq s) \\mid n \\in \\mathcal{N} \\}$\n\\STATE $Q \\coloneqq \\text{a queue holding only } s$\n\\WHILE{$\\neg\\text{Empty}(Q)$}\n \\STATE $n \\coloneqq \\text{Dequeue}(Q)$\n \\FORALL{$(n, m) \\in \\mathcal{E}$}\n \\IF{$\\neg\\text{marked}[m]$}\n \\STATE $\\text{marked}[m] \\coloneqq \\text{true}$\n \\STATE $\\text{Enqueue}(Q, m)$\n \\ENDIF\n \\ENDFOR\n\\ENDWHILE\n\\end{algorithmic}\n\\end{algorithm}"
Algorithm 6 BFS(G, s)
Require: G = ( N , E ) , s ∈ N G = (\mathcal{N}, \mathcal{E}), s \in \mathcal{N} G = ( N , E ) , s ∈ N
1: marked ≔ { n ↦ ( n ≠ s ) ∣ n ∈ N } \text{marked} \coloneqq \{ n \mapsto (n \neq s) \mid n \in \mathcal{N} \} marked : = { n ↦ ( n = s ) ∣ n ∈ N }
2: Q ≔ a queue holding only s Q \coloneqq \text{a queue holding only } s Q : = a queue holding only s
3: while ¬ Empty ( Q ) \neg\text{Empty}(Q) ¬ Empty ( Q ) do
4: n ≔ Dequeue ( Q ) n \coloneqq \text{Dequeue}(Q) n : = Dequeue ( Q )
5: for all ( n , m ) ∈ E (n, m) \in \mathcal{E} ( n , m ) ∈ E do
6: if ¬ marked [ m ] \neg\text{marked}[m] ¬ marked [ m ] then
7: marked [ m ] ≔ true \text{marked}[m] \coloneqq \text{true} marked [ m ] : = true
8: Enqueue ( Q , m ) \text{Enqueue}(Q, m) Enqueue ( Q , m )
9: end if
10: end for
11: end while
Single-source shortest path
Given an undirected graph without weight and node s ∈ N s \in \mathcal{N} s ∈ N s s s s s s
"\\begin{algorithm}\n\\caption{BFS-SSSP(G, s)}\n\\begin{algorithmic}\n\\REQUIRE $G = (\\mathcal{N}, \\mathcal{E}), s \\in \\mathcal{N}$\n\\STATE $\\text{distance} \\coloneqq \\{ n \\mapsto \\infty \\mid n \\in \\mathcal{N} \\}$\n\\STATE $\\text{distance}[s] \\coloneqq 0$\n\\STATE $Q \\coloneqq \\text{a queue holding only } s$\n\\WHILE{$\\neg\\text{Empty}(Q)$}\n \\STATE $n \\coloneqq \\text{Dequeue}(Q)$\n \\FORALL{$(n, m) \\in \\mathcal{E}$}\n \\IF{$\\text{distance}[m] = \\infty$}\n \\STATE $\\text{distance}[m] \\coloneqq \\text{distance}[n] + 1$\n \\STATE $\\text{Enqueue}(Q, m)$\n \\ENDIF\n \\ENDFOR\n\\ENDWHILE\n\\end{algorithmic}\n\\end{algorithm}"
Algorithm 7 BFS-SSSP(G, s)
Require: G = ( N , E ) , s ∈ N G = (\mathcal{N}, \mathcal{E}), s \in \mathcal{N} G = ( N , E ) , s ∈ N
1: distance ≔ { n ↦ ∞ ∣ n ∈ N } \text{distance} \coloneqq \{ n \mapsto \infty \mid n \in \mathcal{N} \} distance : = { n ↦ ∞ ∣ n ∈ N }
2: distance [ s ] ≔ 0 \text{distance}[s] \coloneqq 0 distance [ s ] : = 0
3: Q ≔ a queue holding only s Q \coloneqq \text{a queue holding only } s Q : = a queue holding only s
4: while ¬ Empty ( Q ) \neg\text{Empty}(Q) ¬ Empty ( Q ) do
5: n ≔ Dequeue ( Q ) n \coloneqq \text{Dequeue}(Q) n : = Dequeue ( Q )
6: for all ( n , m ) ∈ E (n, m) \in \mathcal{E} ( n , m ) ∈ E do
7: if distance [ m ] = ∞ \text{distance}[m] = \infty distance [ m ] = ∞ then
8: distance [ m ] ≔ distance [ n ] + 1 \text{distance}[m] \coloneqq \text{distance}[n] + 1 distance [ m ] : = distance [ n ] + 1
9: Enqueue ( Q , m ) \text{Enqueue}(Q, m) Enqueue ( Q , m )
10: end if
11: end for
12: end while
